publications

2025

1. 

   Low-Degree Lower Bounds via Almost Orthonormal Bases

   Alexandra Carpentier, Simone Maria Giancola, Christophe Giraud, and Nicolas Verzelen

   arXiv, Sep 2025

   Abs HTML PDF

   Low-degree polynomials have emerged as a powerful paradigm for providing evidence of statistical-computational gaps across a variety of high-dimensional statistical models [Wein25]. For detection problems – where the goal is to test a planted distribution {}mathbb{P}’ against a null distribution {}mathbb{P} with independent components – the standard approach is to bound the advantage using an {}mathbb{L}^2(}mathbb{P})\-orthonormal family of polynomials. However, this method breaks down for estimation tasks or more complex testing problems where {}mathbb{P} has some planted structures, so that no simple {}mathbb{L}^2(}mathbb{P})\-orthogonal polynomial family is available. To address this challenge, several technical workarounds have been proposed [SW22,SW25], though their implementation can be delicate. In this work, we propose a more direct proof strategy. Focusing on random graph models, we construct a basis of polynomials that is almost orthonormal under {}mathbb{P} in precisely those regimes where statistical-computational gaps arise. This almost orthonormal basis not only yields a direct route to establishing low-degree lower bounds, but also allows us to explicitly identify the polynomials that optimize the low-degree criterion. This, in turn, provides insights into the design of optimal polynomial-time algorithms. We illustrate the effectiveness of our approach by recovering known low-degree lower bounds, and establishing new ones for problems such as hidden subcliques, stochastic block models, and seriation models.

2024

1. 

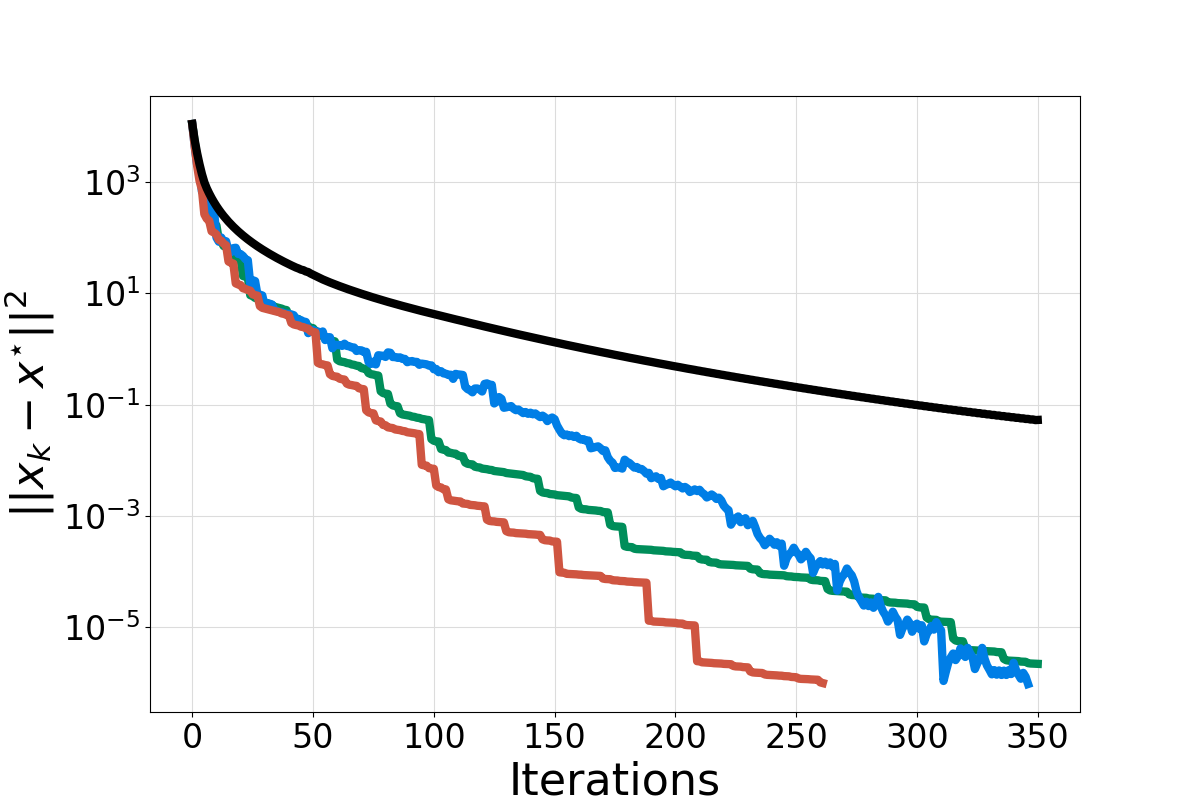   Local Curvature Descent: Squeezing More Curvature out of Standard and Polyak Gradient Descent

   Peter Richtárik, Simone Maria Giancola, Dymitr Lubczyk, and Robin Yadav

   NeurIPS25, May 2024

   Abs Bib HTML PDF

   We contribute to the growing body of knowledge on more powerful and adaptive stepsizes for convex optimization, empowered by local curvature information. We do not go the route of fully-fledged second-order methods which require the expensive computation of the Hessian. Instead, our key observation is that, for some problems (e.g., when minimizing the sum of squares of absolutely convex functions), certain local curvature information is readily available, and can be used to obtain surprisingly powerful matrix-valued stepsizes, and meaningful theory. In particular, we develop three new methods–LCD1, LCD2 and LCD3–where the abbreviation stands for local curvature descent. While LCD1 generalizes gradient descent with fixed stepsize, LCD2 generalizes gradient descent with Polyak stepsize. Our methods enhance these classical gradient descent baselines with local curvature information, and our theory recovers the known rates in the special case when no curvature information is used. Our last method, LCD3, is a variable metric version of LCD2; this feature leads to a closed-form expression for the iterates. Our empirical results are encouraging, and show that the local curvature descent improves upon gradient descent.

   @article{richtarikLocalCurvatureDescent2024,
     title = {Local {{Curvature Descent}}: {{Squeezing More Curvature}} out of {{Standard}} and {{Polyak Gradient Descent}}},
     shorttitle = {Local {{Curvature Descent}}},
     author = {Richt{\'a}rik, Peter and Giancola, Simone Maria and Lubczyk, Dymitr and Yadav, Robin},
     year = {2024},
     month = may,
     number = {arXiv:2405.16574},
     eprint = {2405.16574},
     eprinttype = {math.OC},
     primaryclass = {math},
     publisher = {arXiv},
     keywords = {Mathematics - Optimization and Control},
     journal = {NeurIPS25},
     doi = {10.48550/arXiv.2405.16574}
   }